شرح درس الدالة الأسية مع تمارين أساسية Fonction exponentielle
هذه مجموعة من دروس الدالة الأسية Fonction exponentielle . بالفيديو تتضمن مفاهيم أساسية وتمارين تطبيقية لا بد للتلميذ أن يتقنها , بمعنى أن ما نقدمه سيكون أرضية إنطلاق صلبة لفهم هذا المحور فلتركز معنا جيدا عزيزي التلميذ .

المحتويات :
- مقمة حول الدوال عموما والدالة الأسية خصوصا .
- توجيهات أساسية لفهم هذا المحور مع شرح بالفيديو للخواص . وتمارين بسيطة تتضمن كيفية تطبيق الخواص الأساسية .
- المعادلات التفاضلية .
- سلسلة تمارين مقترحة لمزيد من التعمق .
- بعض إستعمالات الدالة الأسية في العلوم الأخرى .
إستكمالا لما بدأه التلميذ من التعرف على دوال جديده والذي بدأه من السنة الرابعة متوسط , ها هو في السنة الثالثة 3 ثانوي يتعرف على دالة جديدة مهمة جدا .
مفهوم الدالة الأسية والخواص الأساسية
المفاهيم الأساسية التي تدرس في هذا الموضع هي :
- مفهوم الدالة الأسية
- النهايات المشهورة والتي تستعمل غالبا في التخلص من حالات عدم التعيين .
- الدالة المشتقة واتجاه التغير
- بيان الدالة الأسية وإشارتها
تعرف الدوال الأسية Fonction exponentielle بالشكل f(x)=a^x , أي ( a أس x ). حيث a عدد حقيقي موجب . إن مجموعة التعريف لهذه الدوال هي كل الأعداد الحقيقية R .
أما الدالة الأسية النيبيرية فهي حالة خاصة من هذه الدوال حيث a = e . يسمى العدد e ثابت أويلر نسبة للعالم ليونهارد أويلر . أو ثابت نابير نسبة للعالم جون نابير . هذا العدد يساوي بالتقريب 2.7182 , وإضافة لكونها معرفة على R فإنها تتميز بأن صورة الصفر هي الواحد , والدالة المشتقة تساوي الدالة الأصلية لها . يرمز لهذه الدالة بالرمز exp ونكتب : f(x)=exp(x)=e^x. تحقق : exp(0)=1 و (exp'(x)=exp(x .
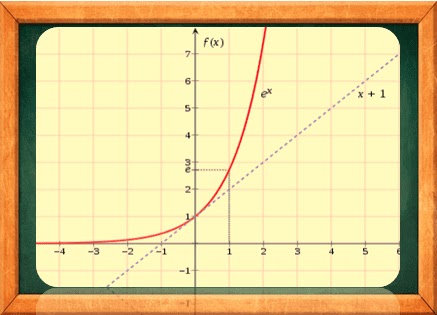
وتتميز الدالة الأسية بأنها دالة موجبة دوما . فمنحناها البياني يقع أعلى محور الفواصل ويقطع محور التراتيب في النقطة ذات الترتيبة 1 , وهي دالة متزايدة دوما على مجال تعريفها .
قواعد الحساب وتمارين حول دراسة دوال أسية
ينتج من خواص الدالة الأسية أن قواعد الحساب عليها هي نفسها قواعد الحساب على الأسس , فينبغي للتلميذ أن يحسن التعامل مع هذه القواعد , والتي سنوضحها في هذا الفيديو . وقد قسمنا الدرس إلى عدة أجزاء .
الدرس الثاني : كيفية إستعمال قواعد الحساب على الدوال الأسية ( الخواص الجبرية ) .
هذه القواعد مهمة جدا وهي من الأشياء الضرورية التي يجب أن يتقنها التلميذ , فهو قد يصادفها في حساب النهايات والمشتقات وفي دراسة الإشارة وقد يصادفها في التكاملات وحساب المساحة , فينبغي أن لا يتهاون التلميذ في هذه القواعد .
الدرس الأول من قواعد الحساب على الدالة الأسية
الدرس الثاني من قواعد الحساب على الدالة الأسية
الدرس الثالث من قواعد الحساب على الدالة الأسية
الدرس الثالث : حل معادلات ومتراجحات تتضمن دوالا أسية .
ومما ينبغي للتلميذ إتقانه هو حل معادلات ومتراجحات تتضمن دوالا أسية . فهي أشياء أساسية جدا في دراسة الدوال الأسية , فالدالة المشتقة تحتاج بشكل أساسي لمعرفة القيم التي تعدمها وكذالك جدول إشارتها
الدرس الرابع : التخلص من حالات عدم التعيين في الدوال الأسية .
ومن الأشياء التي ينبغي للتلميذ إتقانها حساب النهايات , والمشكلة التي تعترض التلميذ أثناء حساب النهايات هي حالات عدم التعيين , والتي نتخلص منها غالبا باستعمال التزايد المقارن .
قد لا يتحصل التلميذ أحيانا أثناء بحثه عن نهاية دالة أسية لحالة من حالات عدم التعيين , فيجد صعوبة في التخلص منها , والغالب أن طريقة التخلص من هذه الحالات تكون باستعمال التزايد المقارن . وقد قمنا بشرح الطرق الأساسية في هذه الدروس .
شاهد كيفية التخلص من حالة عدم التعيين بطريقة التفكيك من هنا
شاهد كيفية التخلص من حالة عدم التعيين بطريقة النشر
شاهد كيفية التخلص من حالات عدم التعيين بطريقة إستخراج العامل المشترك
درس كيفية إشتقاق دوال أسية
من الأشياء المهمة التي لا بد أن يتقنها التلميذ جيدا كيفية إشتقاق دالة أسية , ويكمن أهمية الموضوع في أن دراسة تغيرات الدوال يعتمد على المشتقة ودراستها . ثم رسم المنحنى وأغلب الأسئلة ترتكز على هذه الأشياء .
إتقان التلميذ لكل ما سبق يعني أن التلميذ قد وصل للمرحلة الأخيرة وهي القدرة على دراسة الدالة دراسة كاملة , بحساب نهاياتها وتعيين جدول تغيراتها ورسم منحناها .