شرح درس خاصية طالس مع مثال تطبيقي Thales theorem
للمزيد من ملفات السنة الرابعة متوسط دروس تمارين إختبارات وضعيات يرجى زيارة هذا القسم
إنتبه عزيزي القارئ .
- شرح الخاصية بالفيديو في الأسفل مع أخذ تمرين تطبيقي - مشاهدة ممتعة ملاحظاتكم تهمنا -
- قبل ذالك أرجوا أن تقرأ هذه التوجيهات المهمة .
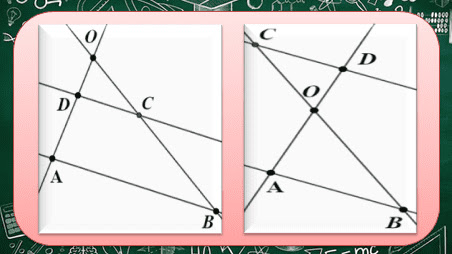
يبدأ التلميذ في التعرف على الخاصية المباشرة في السنة الثالثة متوسط , والتي تنطلق من إفتراض وجود مستقيمين (AB ) و (CD ) متوازيين , يقطعهما مستقيمان آخران (OA ) و ( OB ) غير متوازيين كما هو موضع في الشكل , في هذه السنة يتعرف التلميذ على شكل واحد فقط هو الشكل الموجود في الجانب الأيسر , ثم في السنة الرابعة متوسط يتعمق التلميذ نوعا ما في هذه النظرية فيتعرف على الشكل الثاني منها الموجود في الجانب الأيمن .
إنتبه :
هندسيا ينتج من هذه المعطيات أي مستقيمين متوازيين يقطعها مستقيمين آخرين غير متوازييين مثلثين , نقول في هذه الحالة أن المثلثين في وضعية طالس , ويتميز هذين المثلثين بكون أطولهما متناسبة , ونقول أيضا أنهما متماثلين .
وفق المعطيات السابقة يوجد شكلين فقط المشار إليهما سابقا . ولكن في التمارين قد يقع تداخل بين الأشكال فيكون الشكل غير واضح ولكنه لا يخرج عن النوعين .
ينبغي أثناء تطبيق أي خاصية معرفة شروطها ونتائجها واستعمالها , فالشروط الأساسية لخاصية طالس Thales theorem المباشرة هي :
- وجود التوازي بين مستقيمين وهو أهم شرط من شروطها .
- إستقامية النقاط , فنتحصل على ثلاث نقاط في استقامية تقابلها ثلاث نقاط أخرى في استقامية , تشترك في نقطة واحدة هي نقطة التقاطع .
ينتج من ذالك مثلثين أطوال أضلاعهما متناسبة , ولكي نكتب هذه النسب بشكل سليم لا بد من تعيين المثلثين ثم معرفة الرأس المشترك بينهما , فإنه يلعب دروا أساسيا في كتابة النسب , شاهد الدرس على الفيديو وستفهم أكثر كيف يتم اختيار الأطوال . أما إستعمال نظرية طالس فهي تستعمل في حساب الأطوال .
ملاحظة : نسمي أحد النسب الثلاث بنسبة التصغير أو التكبير بين المثلثين الناتجين .
إذا كنت أستاذا فانتبه فإن بعض التلاميذ لا يحسنون تعيين الرأس المشترك , مما يؤدي إلى الخلط بين النقاط وبالتالي الخطأ في كتابة النسب المتساوية , وربما تجد آخرين لا يحسنون تطبيق الرابع المتناسب . فهذه جزئيات لا بد أن تعتني بها جيدا والتركيز عليها مع التلاميذ